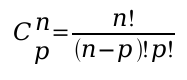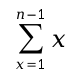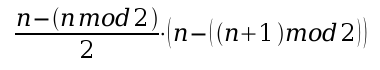Cheers!

Yoan Blanc — Sun, 29 Oct 2006 — , ,

Yesterday night, a friend of mine and I discussed how to know how many glasses are touching each other when you says “Cheers!” before drinking.

It’s a simple combinaison written like that like you learn it at school. p is 2 and n is the number of friends you have (you included).

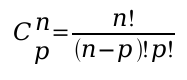
combinaison of 2 in n

But for this simple example where p is set to 2, this big equation with lots of ! inside it, can be written like a sum.

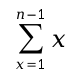
sum from 1 to n minus 1

But a sum isn’t very friendly to a computer. It’s not bad but you can do this better. My solution abuse of the modulo function.

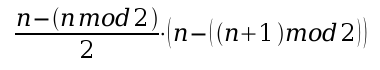
a simple calc for computer

It’s probably clearer in Python. 

cheers = lambda x: (x/2) * (x-(x+1)%2)

You’ll discover some cool things like : 

10 → 45
100 → 4950
1,000 → 499,500
1,0000 → 49,995,000

or 

20 → 190
200 → 19,900
2,000 → 1,999,000
2,0000 → 199,990,000

Have fun!

Hier soir, en rentrant de soirée nous est venu la question du nombre de fois que deux verres font se toucher en fonction du nombre de personnes qu’il y a autour de la table. Ce sont des mathématiques dites simples où il est question de dénombrement. Ici, nous intéresse le nombre de combinaisons de 2 (p) dans une population de n. Qui s’écrit :

combinaisons de p dans n

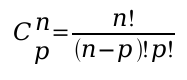
Tout ceci peut revient à faire la somme de 1 à n-1 (comme p vaut 2) :

somme des x de 1 à n moins 1

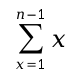
Une fois de plus, ce n’est pas un calcul très convivial pour une machine étant donné que la complexité est de l’ordre de O(n2). Il y a de quoi faire plus simple, j’ai trouvé ça sous ma douche ce matin donc, il y a certainement mieux encore.

le nombre pair le plus proche de n divisé par 2, fois le nombre impair le plus proche de n

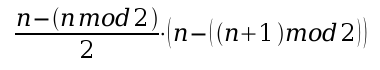
Qui revient à dire : le nombre pair le plus proche de n divisé par 2, fois le nombre impair le plus proche de n. En Python (notez la division entière) : 

cheers = lambda x: (x/2) * (x-(x+1)%2)

En jouant avec cette fonction, il y a des valeurs intéressantes qui peuvent sortir.

Digg it!, so del.icio.us, blogmarks, reddit.